Binary Tree
Binary Tree & Binary Search Tree
如何新建树
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
//方法一:
TreeNode() {}
//方法二:
TreeNode(int val) { this.val = val; }
//方法三:
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
###二叉树的遍历
<font size = 2.5>
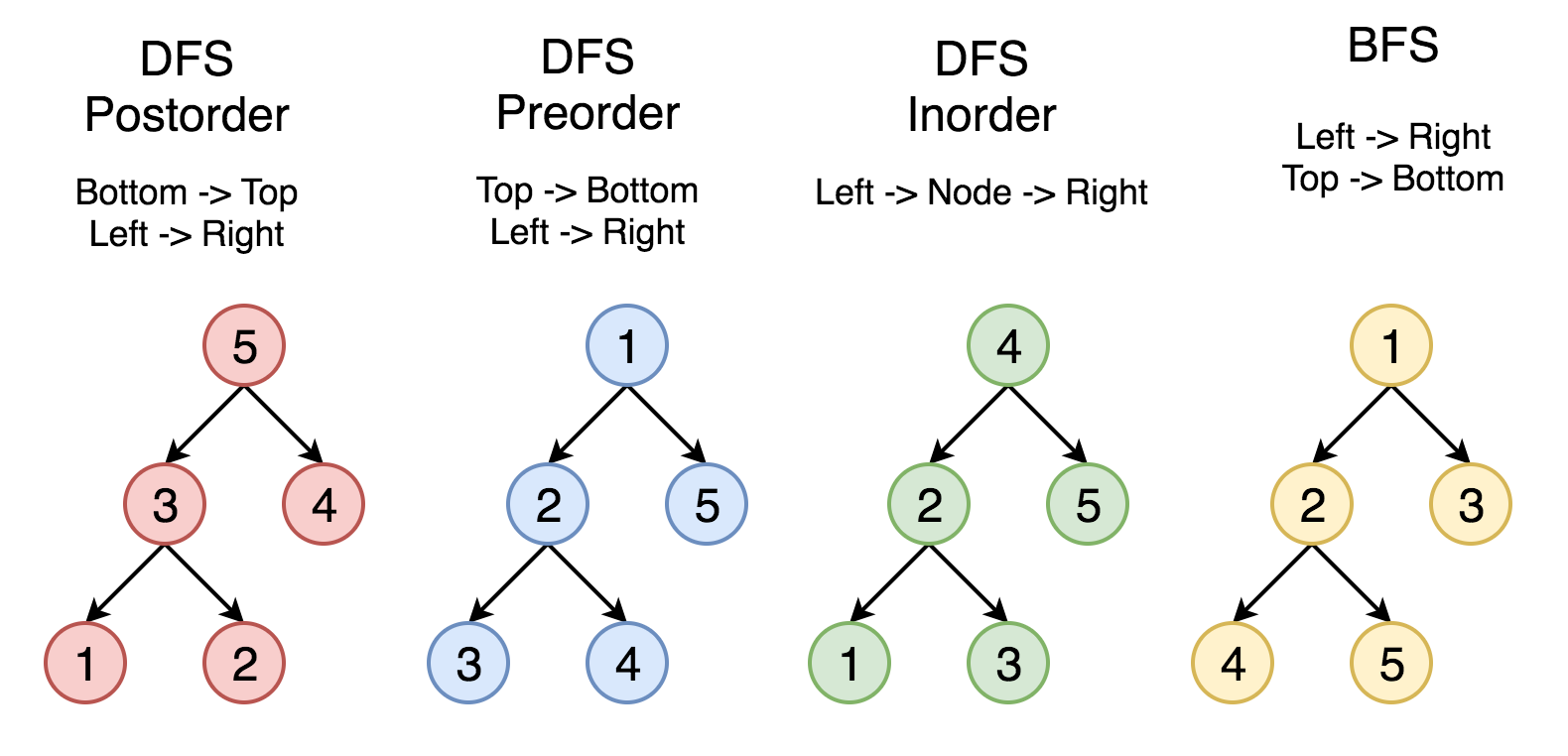
四种主要的遍历思想为:-
前序遍历:根结点 —> 左子树 —> 右子树
-
中序遍历:左子树—> 根结点 —> 右子树
-
后序遍历:左子树 —> 右子树 —> 根结点
-
层次遍历:只需按层次遍历即可
参考(颜色标记法):https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/yan-se-biao-ji-fa-yi-chong-tong-yong-qie-jian-ming/
1.二叉树的前序遍历(Binary Tree Preorder Traversal)
JAVA实现
//方法一:递归
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
preorder(root, res);
return res;
}
public void preorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
res.add(root.val);
preorder(root.left, res);
preorder(root.right, res);
}
}
//时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
//空间复杂度:O(n),为递归过程中栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
//方法二:迭代
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
while (node != null) {
res.add(node.val);
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
return res;
}
}
//时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
//空间复杂度:O(n),为递归过程中显式栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
2.二叉树的中序遍历(Binary Tree Inorder Traversal)
JAVA实现
//方法一:递归
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
inorder(root, res);
return res;
}
public void inorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
//时间复杂度:O(n),其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
//空间复杂度:O(n)。空间复杂度取决于递归的栈深度,而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。
//方法二:迭代
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// 栈 先进后出
// 前序遍历,出栈顺序:根左右; 入栈顺序:右左根
// 中序遍历,出栈顺序:左根右; 入栈顺序:右根左
// 后序遍历,出栈顺序:左右根; 入栈顺序:根右左
List<Integer> res = new ArrayList<Integer>();
Deque<TreeNode> stack = new LinkedList<TreeNode>();
// root为空且stack为空,遍历结束
while (root != null || !stack.isEmpty()) {
// 先根后左入栈
while (root != null) {
stack.push(root);
root = root.left;
}
// 此时root==null,说明上一步的root没有左子树
// 1. 执行左出栈。因为此时root==null,导致root.right一定为null
// 2. 执行下一次外层while代码块,根出栈。此时root.right可能存在
// 3a. 若root.right存在,右入栈,再出栈
// 3b. 若root.right不存在,重复步骤2
root = stack.pop();
res.add(root.val);
root = root.right;
}
return res;
}
}
//时间复杂度:O(n),其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
//空间复杂度:O(n)。空间复杂度取决于栈深度,而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。
3.二叉树的后序遍历(Binary Tree Postorder Traversal)
JAVA实现
//方法一:递归
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
postorder(root, res);
return res;
}
public void postorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
}
//时间复杂度:O(n),其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
//空间复杂度:O(n),为递归过程中栈的开销,平均情况下为 O(log n),最坏情况下树呈现链状,为 O(n)。
//方法二: 迭代
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode prev = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (root.right == null || root.right == prev) {
res.add(root.val);
prev = root;
root = null;
} else {
stack.push(root);
root = root.right;
}
}
return res;
}
}
//时间复杂度:O(n),其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
//空间复杂度:O(n),为迭代过程中显式栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
//为什么官方的迭代奇奇怪怪的,后序遍历不就是前序遍历的翻转吗,前序遍历是往后加元素,后序遍历是往前加元素
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Deque<TreeNode> stack = new LinkedList<>();
LinkedList<Integer> ans = new LinkedList<>();
if (null == root) return ans;
stack.addFirst(root);
while(!stack.isEmpty()) {
TreeNode node = stack.removeFirst();
ans.addFirst(node.val);
if (null != node.left) {
stack.addFirst(node.left);
}
if (null != node.right) {
stack.addFirst(node.right);
}
}
return ans;
}
}