Heap & Graph

Heap & Graph Search Algorithms |

Heap

<font size = 2.5>

Heap: is an unsorted array but have special rules to follow Heapify（数组建堆 时间复杂度O(n)）: https://www.geeksforgeeks.org/building-heap-from-array/

//新建小根堆
PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
//新建大根堆
PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new Comparator<Integer>() {
    public int compare(Integer num1, Integer num2) {
        return num2 - num1;
    }
});

性质：堆的实现通过构造二叉堆(binary heap)，这种数据结构具有以下性质

  1. 任意节点小于它的所有后裔，最小元素在堆的根上 (增序性)。
  2. 堆总是一颗完全树。Complete tree
  3. 将根节点最大的堆叫做MAX HEAP, 根节点最小的堆叫做最小堆MIN HEAP
  4. Index of lChild = index of parent X 2 + 1
  5. Index of rChild = index of parent X 2 + 2
  6. Unsorted but follow rules above

支持的基本操作：

  1. Insert: 向堆中植入一个新元素；时间复杂度o(log(n)) insert 0
  2. Update: 将新元素提升使其符合堆的性质， 时间复杂度o(log(n)) 4 -> -4 3 -> 13
  3. Get/top: 获取当前堆顶元素的值；时间复杂度o(1)
  4. Pop: 删除堆顶元素； 时间复杂度o(log(n))
  5. Heaplfy: 使用一个unsorted array变成一个堆。时间复杂度o(n)

Example

1.未排序数组中最小的k位数。 Find smallest k elements from an unsorted array of size n. JAVA实现

//方法一：排序后取前k位
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        int[] vec = new int[k];
        Arrays.sort(arr);
        for (int i = 0; i < k; ++i) {
            vec[i] = arr[i];
        }
        return vec;
    }
}

//方法二：堆
//1. minHeap
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        int[] result = new int[k];
        // Corner case
        if (k == 0) return result;
        PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
        for (int i = 0; i < arr.length; i++) {
            minHeap.offer(arr[i]);
        }
        for (int i = 0; i < k; i++) {
            result[i] = minHeap.poll();
        }
        return result;
    }
}

//2. maxHeap
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        int[] result = new int[k];
        if (k == 0) { // 排除 0 的情况
            return result;
        }

        //java priority queue默认小根堆，实现大根堆需要重写一下比较器。
        PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new Comparator<Integer>() {
            public int compare(Integer num1, Integer num2) {
                return num2 - num1;
            }
        });
/**
实现大根堆也可以写成：
PriorityQueue<Integer>priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });
**/

        for (int i = 0; i < k; ++i) {
            maxHeap.offer(arr[i]);
        }
        for (int i = k; i < arr.length; ++i) {
            if (maxHeap.peek() > arr[i]) {
                maxHeap.poll();
                maxHeap.offer(arr[i]);
            }
        }
        for (int i = 0; i < k; ++i) {
            result[i] = maxHeap.poll();
        }
        return result;
    }
}

题解地址： https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/solution/jian-zhi-offer-40-zui-xiao-de-k-ge-shu-j-9yze/

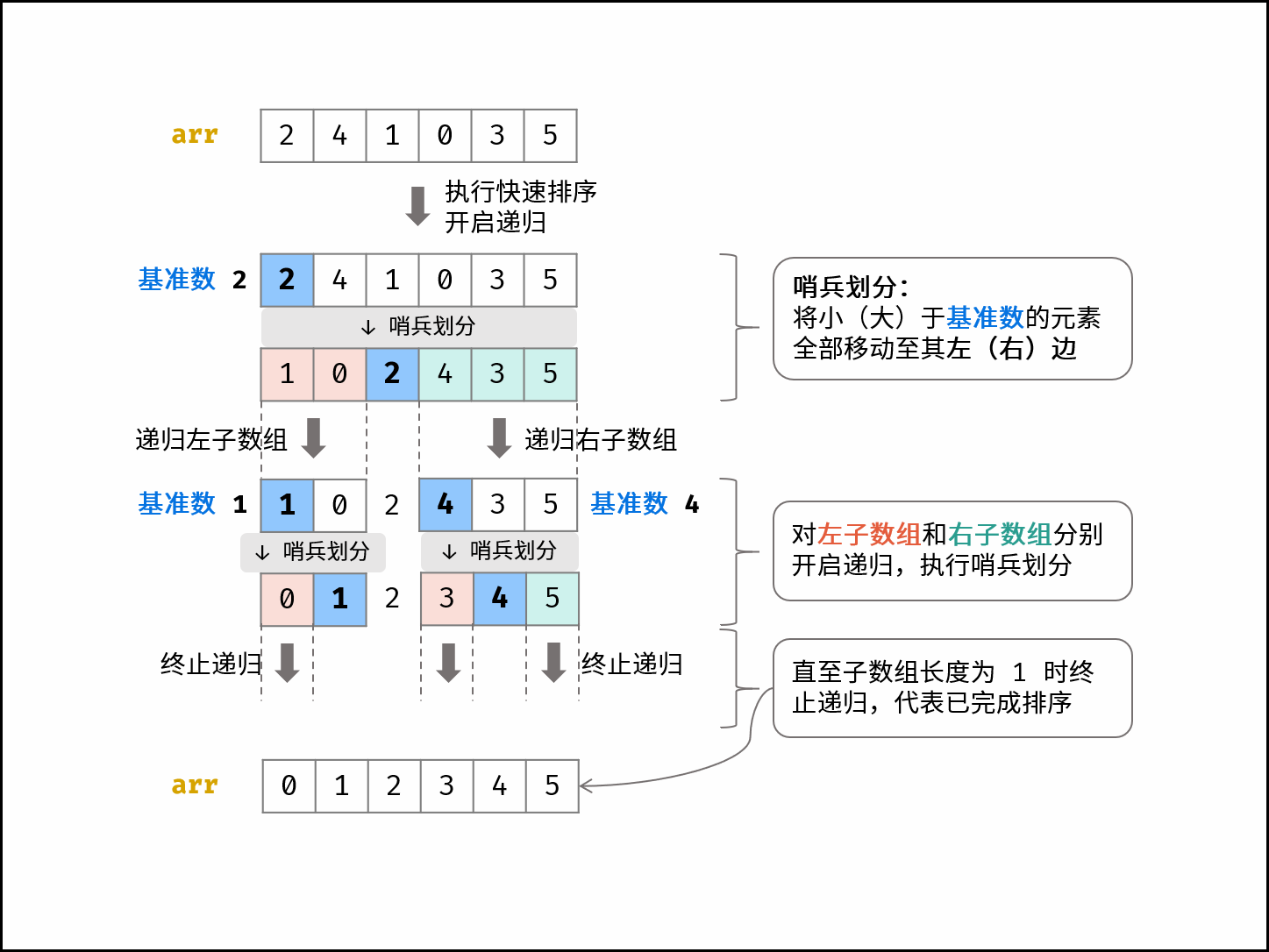
avatar

//快排
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        quickSort(arr, 0, arr.length - 1);
        //返回数组的前k个值
        //对于原始数组和新数组中有效的所有索引，两个数组将具有相同的值。
        //如果复制的数组长度大于原始数组的长度，则原始索引中丢失的索引的副本数将为零。
        return Arrays.copyOf(arr, k);
    }
    private void quickSort(int[] arr, int l, int r) {
        // 子数组长度为 1 时终止递归
        if (l >= r) return;
        // 哨兵划分操作（以 arr[l] 作为基准数）
        int i = l, j = r;
        while (i < j) {
            while (i < j && arr[j] >= arr[l]) j--;
            while (i < j && arr[i] <= arr[l]) i++;
            swap(arr, i, j);
        }
        swap(arr, i, l);
        // 递归左（右）子数组执行哨兵划分
        quickSort(arr, l, i - 1);
        quickSort(arr, i + 1, r);
    }
    private void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

</font>

Graph

<font size = 2.5>

results matching ""

    No results matching ""